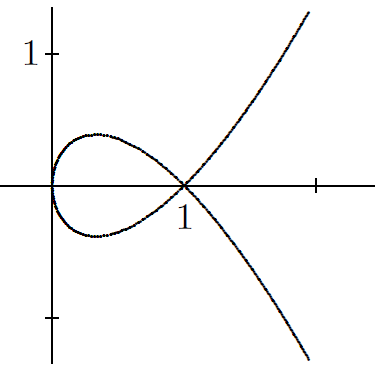Theme-Based Curriculum
Exeter’s match curriculum and problem sets focus on recurring strands, each of which grows in sophistication as your skills and knowledge increase and broaden.
Strands that arise throughout our problem sets include:
Optimization
Optimization problems arise in a variety of settings throughout our problems sets. Here are a few examples.
Math 1: Robin works part-time carving wooden seagulls and lobsters to sell to tourists during the summer season. Keeping up with demand means carving at least two seagulls and three lobsters a day. Robin can produce at most a dozen models a day. Can Robin make a profit of $70 in one day? What combination of seagulls and lobsters produces the greatest daily profit? What is this maximum profit?
(Math 1, #566)
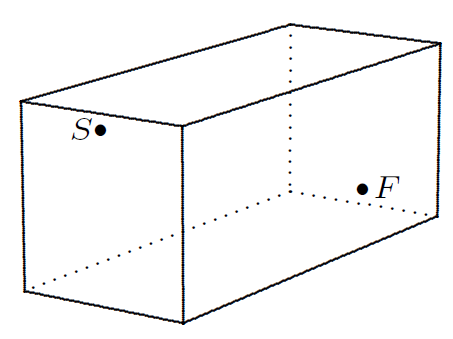 Math 2: A spider lived in a room that measured 30 feet long by 12 feet wide by 12 feet high. One day, the spider spied an incapacitated fly across the room, and of course wanted to crawl to it as quickly as possible. The spider was on an end wall, one foot from the ceiling and six feet from each of the long walls. The fly was stuck one foot from the floor on the opposite wall, also midway between the two long walls. Knowing some geometry, the spider cleverly took the shortest possible route to the fly and ate it for lunch. How far did the spider crawl?
Math 2: A spider lived in a room that measured 30 feet long by 12 feet wide by 12 feet high. One day, the spider spied an incapacitated fly across the room, and of course wanted to crawl to it as quickly as possible. The spider was on an end wall, one foot from the ceiling and six feet from each of the long walls. The fly was stuck one foot from the floor on the opposite wall, also midway between the two long walls. Knowing some geometry, the spider cleverly took the shortest possible route to the fly and ate it for lunch. How far did the spider crawl?
(Math 2, 24#2)
Math 3: The diameter and the slant height of a cone are both 24 cm. Find the radius of the largest sphere that can be placed inside the cone. (The sphere is therefore tangent to the base of the cone.) The sphere occupies a certain percentage of the cone’s volume. First estimate this percentage, then calculate it.
(Math 3, 29#5)
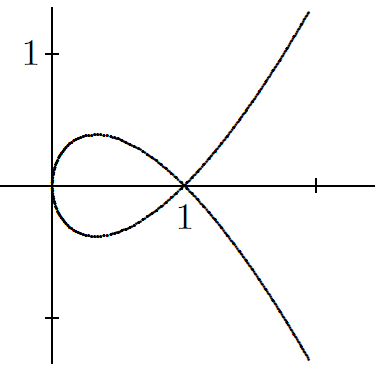 Math 4: Verify that the curve y2 + 2x2 = x3 + x is traced parametrically by x = t2 and y = t3 – t. Use these two equations to find the slope of the line that is tangent to the curve at (4, 6). Find coordinates for the two points on the curve where the y-coordinate is locally extreme.
Math 4: Verify that the curve y2 + 2x2 = x3 + x is traced parametrically by x = t2 and y = t3 – t. Use these two equations to find the slope of the line that is tangent to the curve at (4, 6). Find coordinates for the two points on the curve where the y-coordinate is locally extreme.
(Math 4, 62#8, image from 62#3)
Symmetry
Symmetry arises in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: A hot-air balloon ride has been set up so that a paying customer is carried straight up at 50 feet per minute for ten minutes and then immediately brought back to the ground at the same rate. The whole ride lasts twenty minutes. Let h be the height of the balloon (in feet) and t be the number of minutes since the ride began. Draw a graph of h versus t. What are the coordinates of the vertex? Find an equation that expresses h in terms of t.
(Math 1, #376)
Math 2: Find as many ways as you can to dissect each figure below into two congruent parts.
(Math 2, 6#10)
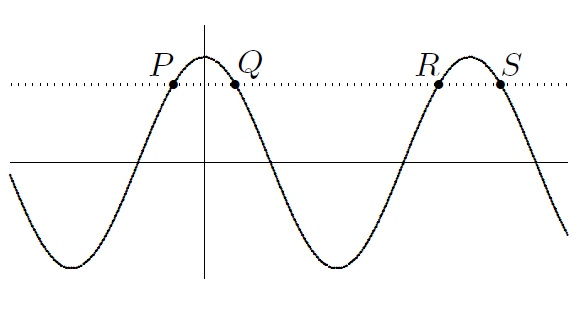
Math 3: Below you see the graphs of y = cos(x) and y = 0.7431 (dotted). Given that Q = (42, 0.7431), find coordinates for the intersection points P, R, and S without using a calculator.
(Math 3, 19#4)
Math 4: Given that function f has the property f(180 − x) = f(x) for all x-values, show that the graph y = f(x) has reflective symmetry. Identify the mirror. Name two such functions.
(Math 4, 4#6)
Rates of Change
Rates of change arise in a variety of settings throughout our problem sets. Here are a few examples.
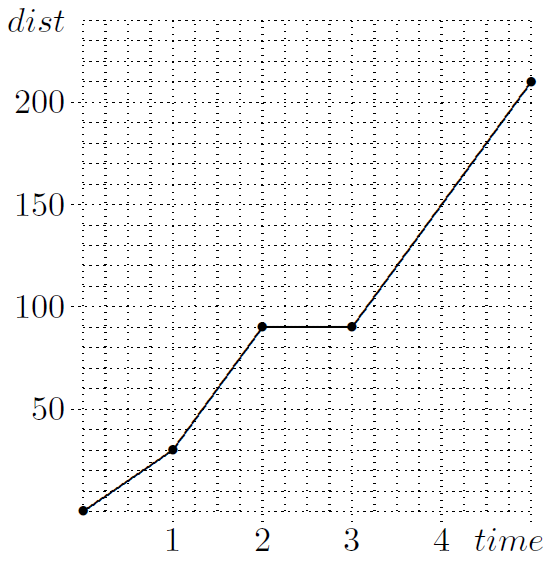
Math 1: Sandy recently made a 210-mile car trip, starting from home at noon. The graph at right shows how Sandy’s distance from home (measured in miles) depends on the number of hours after noon. Make up a story that accounts for the four distinct parts of the graph. In particular, identify the speed at which Sandy spent most of the afternoon driving.
(Math 1, #143)
Math 2: An Unidentified Flying Object (UFO) moving along a line with constant speed was sighted at (8, 9, 10) at noon and at (13, 19, 20) at 1:00 pm. Where was the UFO at 12:20 pm? When, and from where, did it leave the ground (z = 0)? What was the UFO’s speed?
(Math 2, 37#6)
Math 3: A spherical balloon is being inflated by a machine that increases the balloon’s volume at a steady 1000 cc per second.
Show that the balloon’s radius after 6.0 sec of inflation is approximately 11.273 cm.
What is the balloon’s radius after 6.1 sec of inflation?
Find approximately the rate (cm/sec) at which the radius is increasing at that instant when the volume reaches 6000 cc.
(Math 3, 54#8)
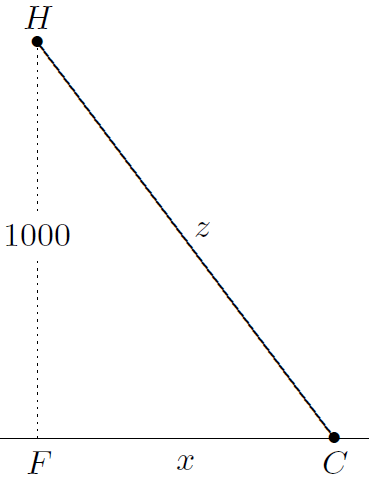
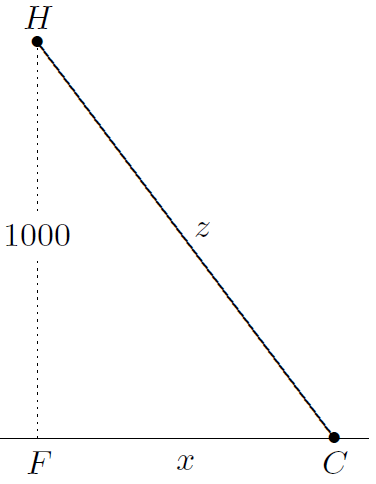 Math 4: A police helicopter H is hovering 1000 feet above a highway, using radar to check the speed of a red convertible C below. The radar shows that distance HC is 1250 feet and increasing at 66 feet per second. The obvious question: Is the car exceeding the speed limit, which is 65 mph? Here is how to figure out the speed of the car: Let x = FC, where F is the point on the highway that is directly beneath H, and let z = HC. Notice that x and z are both functions of t, and that z(t)2 = 10002 + x(t)2 . Differentiate both sides of this equation with respect to t. The new equation involves dx/dt and dz/dt as well as x and z. The radar shows that dz/dt = 66 when z = 1250. Use this data to calculate dx/dt.
Math 4: A police helicopter H is hovering 1000 feet above a highway, using radar to check the speed of a red convertible C below. The radar shows that distance HC is 1250 feet and increasing at 66 feet per second. The obvious question: Is the car exceeding the speed limit, which is 65 mph? Here is how to figure out the speed of the car: Let x = FC, where F is the point on the highway that is directly beneath H, and let z = HC. Notice that x and z are both functions of t, and that z(t)2 = 10002 + x(t)2 . Differentiate both sides of this equation with respect to t. The new equation involves dx/dt and dz/dt as well as x and z. The radar shows that dz/dt = 66 when z = 1250. Use this data to calculate dx/dt.
(Math 4, 48#6)
Graphical Representations
Graphical representations arise in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: A cylindrical container is filled to a depth of d cm by pouring in V cc of liquid. Draw a plausible graph of d versus V. Recall that d versus V means that V is on the horizontal axis.
(Math 1, #752)
Math 2: Find an equation that says that P = (x, y) is equidistant from F = (2, 0) and the y-axis. Plot four points that fit this equation. The configuration of all such points P is called a parabola.
(Math 2, 33#1)
Math 3: Interpreted in degree mode, the equation y = 0.3cos(36000t)sin(x) models the motion of a stretched, vibrating string that is 180 centimeters long (x = 0 is one end of the string and x = 180 is the other). The amplitude of the vibration is 0.3 cm.
Verify that the period of the vibration is 0.01 second. This means that the string vibrates 100 times per second.
Taking a photo of the string corresponds to choosing a t-value. For example, the diagram shows the string at the instant t = 0. Notice that the amplitude has been exaggerated to make it more visible. Sketch photos of the string for t = 0.001, t = 0.0025, t = 0.003, and t = 0.005 second.

How far does the center of the string move during one complete vibration? Does the center of the string move with constant speed? Calculate an approximate value for the speed of the center of the string when t = 0.0025 second.
(Math 3, 70#5)
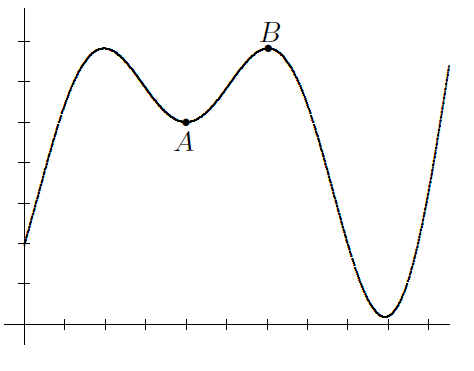
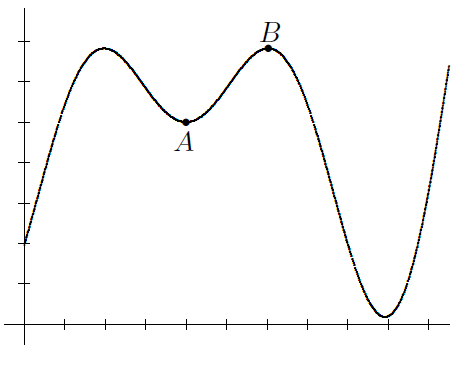 Math 4: The diagram shows the graph of y = f(x), which can be interpreted in the following two ways:
Math 4: The diagram shows the graph of y = f(x), which can be interpreted in the following two ways:
It shows the elevation during a hike along a mountain ridge, as a function of time. During the part of the hike represented by the curve that joins point A to point B, there is a moment when the hiker is working hardest. If you had a formula for the function f, how would you calculate this time?
(b) It represents a bird’s-eye view of a winding road. As you drive along the section of road from point A towards point B, there is a point where the car stops turning to the left and starts turning to the right. If you had a formula for the function f, how would you locate this point?
(Math 4, 50#7)
Vectors and Parameterization
Vectors and parametric representations of points arise in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: From its initial position at (−1, 12), a bug crawls linearly with constant speed and direction. It passes (2, 8) after two seconds. How much time does the bug spend in the first quadrant?
(Math 1, #872)
Math 2: A direction vector for a line is any vector that joins two points on that line. Find a direction vector for 2x + 5y = 8. It is not certain that you and your classmates will get exactly the same answer. How should your answers be related, however?
(Math 2, 20#8)
Math 3: Graph the curve that is described parametrically by (x, y) = (5cost, 4sint). If you are working in degree mode, the parameter interval should of course be 0 ≤ t ≤ 360. This presentation should remind you of the parametric description of a circle. The curve is actually an ellipse. Confirm this by substituting the parametric equations into the ellipse equation 16x2 + 25y2 = 400.
(Math 3, 46#7)
Math 4: The curve (x, y) = (t2, t3 − t) is shown at right. Find the area enclosed by the loop in the graph.
(Math 4, 74#9)
Modeling
Mathematical models arise in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: Chris does a lot of babysitting. When parents drop off their children and Chris can supervise them at home, the hourly rate is $3. If Chris has to travel to the child’s home, there is a fixed charge of $5 for transportation in addition to the $3 hourly rate.
- Graph y = 3x and y = 3x + 5. What do these lines have to do with the babysitting context? What feature do they have in common? How do they differ?
- What does the graph of y = 3x + 6 look like? What change in the babysitting context does this line suggest?
(Math 1, #193)
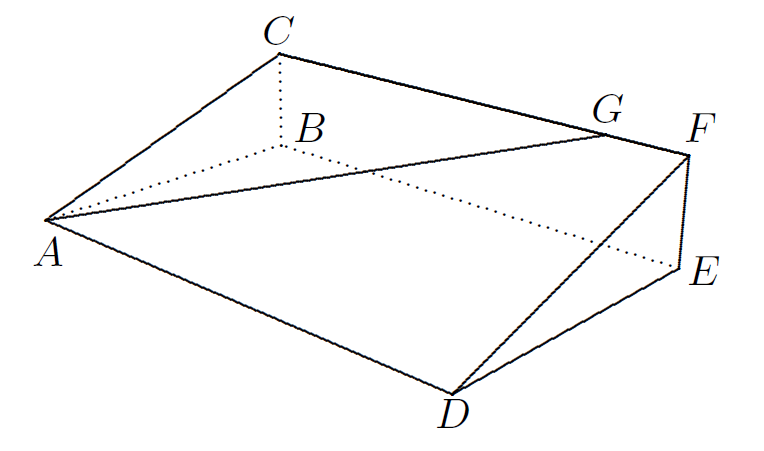
Math 2: Peyton’s workout today is to run repeatedly up a steep grassy slope, represented by ADFC in the diagram. The workout loop is AGCA, in which AG requires exertion and GCA is for recovery. Point G was chosen on the ridge CF to make the slope of the climb equal 1/5. Given that ADEB and BEFC are rectangles, ABC is a right angle, AD = 240, DE = 150, and EF = 50, find the distance from point G to point C.
(Math 2, 75#9)
Math 3: Suppose that three PEA students know a certain rumor at noon, that there are 1000 students in all, and that any student will try to pass a rumor along to one more student each hour. This suggests the model , where is the number of students who know the rumor hours after noon. It is given that = 3. The fraction in the recursive equation represents that portion of the student body that does not know the rumor. Calculate , , and . Your answers will suggest the equation , which describes 100% growth. Explain why this model becomes less realistic as n increases.
(Math 3, 77#3)
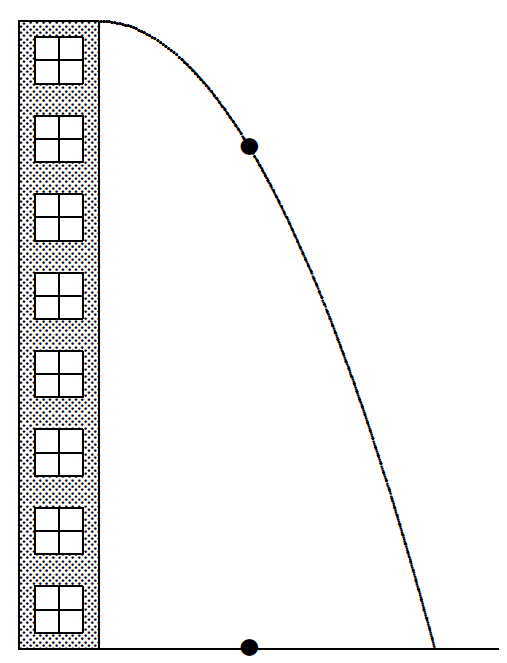 Math 4: After being thrown from the top of a tall building, a projectile follows the path (x, y) = (60t, 784 − 16t2), where x and y are in feet and t is in seconds. The Sun is directly overhead, so that the projectile casts a moving shadow on the ground beneath it, as shown in the figure.
Math 4: After being thrown from the top of a tall building, a projectile follows the path (x, y) = (60t, 784 − 16t2), where x and y are in feet and t is in seconds. The Sun is directly overhead, so that the projectile casts a moving shadow on the ground beneath it, as shown in the figure.
When t = 1, how fast is the shadow moving? How fast is the projectile losing altitude? How fast is the projectile moving?
What is the altitude of the projectile when t = 2? What is the altitude of the projectile a little later, when t = 2 + k? How much altitude is lost during this k-second interval? At what rate is the projectile losing altitude during this interval?
(Math 4, 11#6)
Transformations
Transformations arise in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: Graph y = |x−5| and y = |x+3|, then describe in general terms how the graph of y = |x| is transformed to produce the graph of y = |x−h|.
(Math 1, #309)
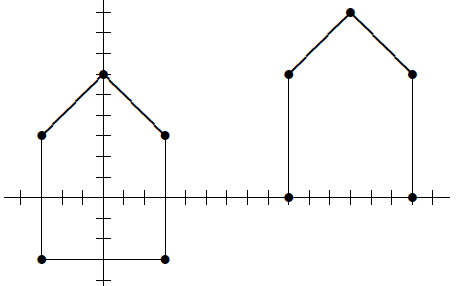
Math 2: ApplyT(x,y) = (2x/3, 2y/3) to the following pentagons:
- vertices (3, −3), (3, 3), (0, 6), (−3, 3), and (−3, −3);
- vertices (15, 0), (15, 6), (12, 9), (9, 6), and (9, 0). Are the results what you expected?
(Math 2, 54#6)
Math 3: Describe the effect of each of the following geometric transformations. To generate and test your hypotheses, transform some simple points.
(a) T(x,y) = (−3x, −3y)
(b) T(x,y) = (−y,x)
(c) T(x,y) = (−y, −x)
(d) T(x,y) = (0.6x− 0.8y, 0.8x+ 0.6y)
(Math 3, 16#6)
Math 4: The slope of the curve y= 2x at its y-intercept is ln(2), which is approximately 0.693. Use this information (but no calculator) to find the slope of the curve y= 3 2x at its y-intercept. Answer the same question for y= 23 2x, then use your result to find the slope of the curve y= 2x at the point (3, 8).
(Math 4, 20#6)